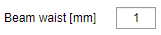Gaussian beam
This function is responsible for the Gaussian beam generation. Where the basic Gaussian beam equation, assuming that the propagation path equals 0 (z=0), is [1]:
\(E(x,y,z=0) = exp\left(\frac{-\rho^2}{w_{0}^2}\right)\), where \(\rho = \sqrt{x^2+y^2}\)
The \(w_{0}\) is a beam waist, which users can control.